一弦法正矢计算

本数据计算依据具体详见一弦法正矢计算一弦法整正曲线四等分法，八等分法各点正矢计算

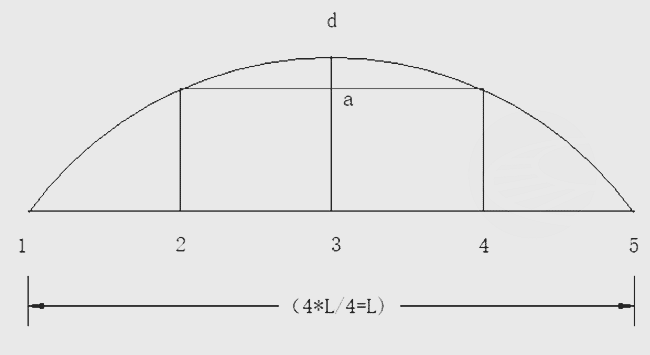
四等分法计算结果

4等分间距(m):
f2及f4矢 距(mm):
f3 矢距(mm):

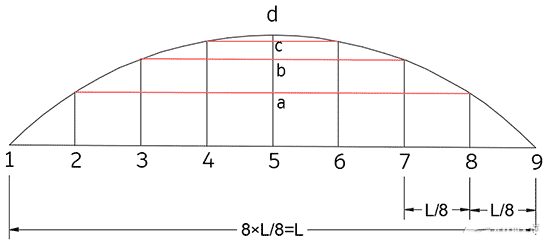
八等分法计算结果

8等分间距(m):
f2及f8矢 距(mm):
f3及f7矢 距(mm):
f4及f6矢 距(mm):
f5 矢 距(mm):

曲线上任意点矢距的计算

如上图所示,设弦长AB=C,如上所述,

$$f=\frac{C^2}{8R}$$

距AB弦始终点为a的任意点的矢距f’,等于正矢f减去以(C-2a)为弦的正矢，即

$${f}’=\frac{C^2}{8R}-\frac{\left (C-2a \right )^2}{8R}\\
=\frac{4aC-4a^2}{8R}=\frac{4a(C-a)}{8R}\\
=\frac{a(C-a)}{2R}$$

如\(a=\frac{1}{8}C\)，则

$${f}’_{1/8}=\left [ \frac{4C}{8}\left ( C-\frac{C}{8}\right )\right ]\div 8R\\
=\frac{4}{8}\times \frac{7}{8}\times \frac{C^2}{8R}=\frac{7}{16}f$$

如\(a=\frac{1}{4}C\)，则

$${f}’_{1/4}=\left [4\times \frac{C}{4}\left ( C-\frac{C}{4}\right )\right ]\div 8R\\
=\frac{3}{4}\times \frac{C^2}{8R}=\frac{3}{4}f=\frac{12}{16}f$$

如\(a=\frac{3}{8}C\)，则

$${f}’_{3/8}=\left [4\times \frac{3C}{8}\left ( C-\frac{3C}{8}\right )\right ]\div 8R\\
=\frac{3}{8}\times \frac{5}{2}\times \frac{C^2}{8R}=\frac{15}{16}f$$