直圆邻测点正矢计算

本数据计算依据具体详见圆曲线直圆点、圆直点邻点正矢在线计算注：距离aλ为示意图中1点至ZY点建的距离；距离bλ为示意图中2点至ZY点建的距离（aλ+bλ=λ=弦长/2）。

1.2 无缓和曲线时，圆曲线始终点处正矢

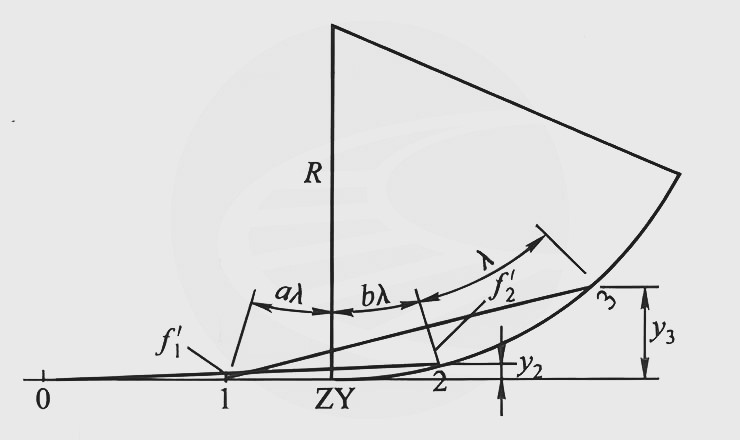
如上图所示，当圆曲线与直线相连时，由于测量弦线的一端伸入到直线内，故圆曲线始、终点ZY、YZ)两侧测点的正矢与圆曲线内的各点不同。

设: 1、2测点的正矢分别为f₁、f₂则

$$f_1=\frac{b^2}{2}f_y\\
f_2=\left (1-\frac{a^2}{2} \right )f_y$$

当a=0、b=1时，1测点为圆曲线始点，则f₁=fy÷2、f₂=fy，即圆曲线始点位于2测点时其正矢为圆曲线正矢的二分之一。

直圆点正矢 \(f_{zy}=\frac{f }{2}\)

圆直点正矢 \(f_{yz}=\frac{f }{2}\)

例:圆曲线计划正矢f=100mm、a=1.5m、b=8.5m（其中10为点间距，比如现场采用20m弦时，点间距为10m）。求f₁、f₂

解：

$$a=\frac{a\lambda }{\lambda}=\frac{1.5}{10}=0.15\\b=\frac{b\lambda }{\lambda}=\frac{8.5}{10}=0.85$$

$$f_1=\frac{b^2}{2}f_y=\frac{0.85^2}{2}\times 100=36.1mm\\
f_2=\left (1-\frac{a^2}{2} \right )f_y=\left (1-\frac{0.15^2}{2} \right )\times 100=98.9mm$$