一、圆曲线正矢的计算(原创:轨魅网)
1.1 圆曲线正矢的计算公式
取圆曲线上两点拉一直线,叫做弦。弦上任意点至曲线上的垂直距离叫矢或叫矢距。在弦中央点的矢距叫正矢(下图)。

AB一弦;AC、CB一半弦;CD一正矢;EF一矢距
正矢计算公式为
$$f=\frac{C^2}{8R}$$
其中: f-正矢 C-弦长 R-半径 式中单位均为m。
公式用文字表示即:正矢=(弦长X弦长)÷(8×半径)
1.2 无缓和曲线时,圆曲线始终点处正矢
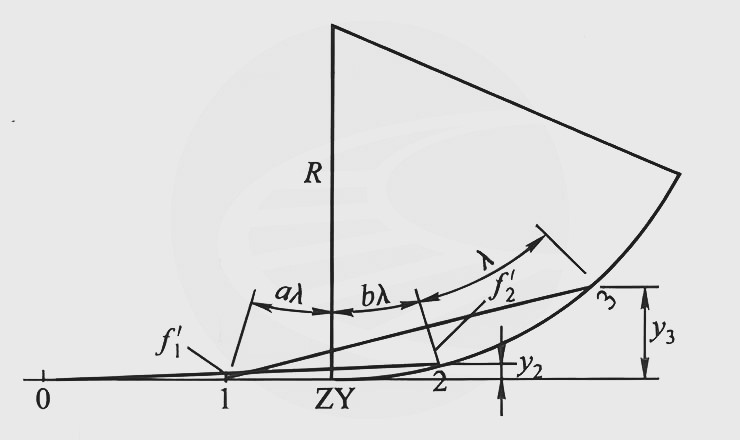
如上图所示,当圆曲线与直线相连时,由于测量弦线的一端伸入到直线内,故圆曲线始、终点ZY、YZ)两侧测点的正矢与圆曲线内的各点不同。
设: 1、2测点的正矢分别为f1、f2则
$$f_1=\frac{b^2}{2}f_y\\
f_2=\left (1-\frac{a^2}{2} \right )f_y$$
当a=0、b=1时,1测点为圆曲线始点,则f1=fy÷2、f2=fy,即圆曲线始点位于2测点时其正矢为圆曲线正矢的二分之一。
直圆点正矢 \(f_{zy}=\frac{f }{2}\)
圆直点正矢 \(f_{yz}=\frac{f }{2}\)
例:圆曲线计划正矢f=100mm、a=1.5m、b=8.5m(其中10为点间距,比如现场采用20m弦时,点间距为10m)。求f1、f2
解:
$$a=\frac{a\lambda }{\lambda}=\frac{1.5}{10}=0.15\\b=\frac{b\lambda }{\lambda}=\frac{8.5}{10}=0.85$$
$$f_1=\frac{b^2}{2}f_y=\frac{0.85^2}{2}\times 100=36.1mm\\
f_2=\left (1-\frac{a^2}{2} \right )f_y=\left (1-\frac{0.15^2}{2} \right )\times 100=98.9mm$$
弦长与正矢的关系
$$f=\frac{C^2}{8R}$$
假如用20m弦,半径为2500m,则正矢=20mm;
假如用10m弦,半径为2500m,则正矢=5mm;
假如用5m弦,半径为2500m,则正矢=1.25mm;
同理,假如半径500m,则
弦长20m时,正矢=100mm;
弦长10m时,正矢=25mm;
弦长5m时,正矢=6.25mm;
根据这两个例题,可以找出弦长与正矢的关系:当半径不变,弦长为原弦长的1/2倍时,正矢为原正矢的1/4倍;弦长为1/4倍时,正矢为1/16倍,因此弦长为n倍时,则正矢为n²倍。
曲线上任意点矢距的计算

如上图所示,设弦长AB=C,如上所述,
$$f=\frac{C^2}{8R}$$
距AB弦始终点为a的任意点的矢距f’,等于正矢f减去以(C-2a)为弦的正矢,即
$${f}’=\frac{C^2}{8R}-\frac{\left (C-2a \right )^2}{8R}\\
=\frac{4aC-4a^2}{8R}=\frac{4a(C-a)}{8R}\\
=\frac{a(C-a)}{2R}$$
如\(a=\frac{1}{8}C\),则
$${f}’_{1/8}=\left [ \frac{4C}{8}\left ( C-\frac{C}{8}\right )\right ]\div 8R\\
=\frac{4}{8}\times \frac{7}{8}\times \frac{C^2}{8R}=\frac{7}{16}f$$
如\(a=\frac{1}{4}C\),则
$${f}’_{1/4}=\left [4\times \frac{C}{4}\left ( C-\frac{C}{4}\right )\right ]\div 8R\\
=\frac{3}{4}\times \frac{C^2}{8R}=\frac{3}{4}f=\frac{12}{16}f$$
如\(a=\frac{3}{8}C\),则
$${f}’_{3/8}=\left [4\times \frac{3C}{8}\left ( C-\frac{3C}{8}\right )\right ]\div 8R\\
=\frac{3}{8}\times \frac{5}{2}\times \frac{C^2}{8R}=\frac{15}{16}f$$
二、缓和曲线正矢的计算
缓和曲线的半径是由无穷大逐渐变为与圆曲线半径相同。由于缓和曲线的半径是变化的,所以缓和曲线上各点正矢都不一样,其变化规律是由始点向圆曲线方向渐次增加一定的量。现将缓和曲线各部正矢的计算分述如下。
2.1 缓和曲线正矢的计算公式
$$f_x=\frac{nf_c}{m}$$
式中
fx——缓和曲线正矢;
n——测点点号;
m——缓和曲线分段数;
fc——圆曲线正矢。

例:设圆曲线正矢为120mm,缓和曲线等分6段(上图),则缓和曲线上各测点的正矢为
$$测点1的正矢=\frac{nf_c}{m}=\frac{1\times 120}{6}=20mm;\\
测点2的正矢=\frac{nf_c}{m}=\frac{2\times 120}{6}=40mm;\\
测点3的正矢=\frac{nf_c}{m}=\frac{3\times 120}{6}=60mm;\\
测点4的正矢=\frac{nf_c}{m}=\frac{4\times 120}{6}=80mm;\\
测点5的正矢=\frac{nf_c}{m}=\frac{5\times 120}{6}=100mm;$$
从上面例子可以看出,缓和曲线各测点正矢递增量是一个常数,即等于圆曲线的正矢除缓和曲线分段数(测点数)。
用公式表示即为
$$缓和曲线各测点递增量=\frac{圆曲线正矢}{缓和曲线分段数}$$
例:圆曲线正矢为120mm,将缓和曲线等分为6段,则每点正矢递增量为
$$递增量f_d=\frac{120}{6}=20mm$$
同上可得
$$测点1的正矢=1×f_d=1×20=20mm\\
测点2的正矢=2×f_d=2×20=40mm\\
测点3的正矢=3×f_d=3×20=60mm\\
测点4的正矢=4×f_d=4×20=80mm\\
测点5的正矢=5×f_d=5×20=100mm$$
2.2 缓和曲线始终点正矢的计算
测点在缓和曲线始终点时,缓和曲线起点(直缓ZH、缓直HZ)的正矢为缓和曲线递增量的六分之一;缓和曲线终点(缓圆HY、圆缓YH)的正矢为圆曲线正矢减去缓和曲线正矢递增量的六分之一(即减去缓和曲线始点的正矢)。
以公式表示为:
$$缓和曲线始点正矢=\frac{缓和曲线正矢递增量}{6}$$
$$缓和曲线终点正矢=圆曲线正矢-缓和曲线始点正矢$$
例:圆曲线正矢为100mm,缓和曲线测点分成5段(即缓和曲线长为50m),缓和曲线的始终点正矢为
缓和曲线的正矢递增量=100÷5=20mm
缓和曲线始点正矢=20÷6≈3mm
缓和曲线终点正矢= 100-20÷6≈97mm
2.3 缓和曲线始点(ZH、HZ)相邻测点的正矢
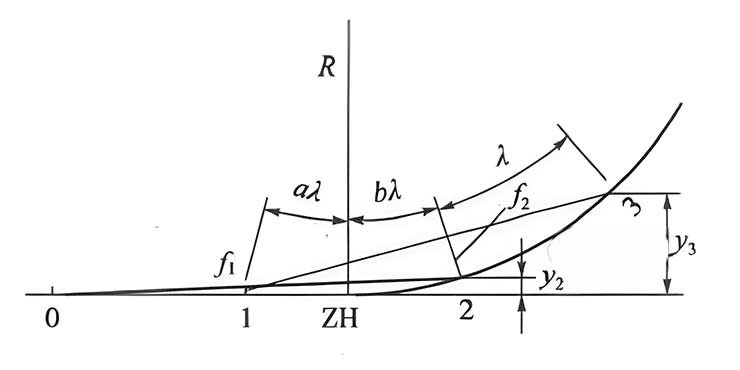
如图所示,设1、2两测点分别在ZH点两侧,与ZH点相距分别为aλ、bλ,λ为测点间的距离,等于弦长的一半,a+b=λ, 则:
公式:
$$f_1=\frac{b^3}{6} f_d \\
f_2=\left (b+\frac{a^3}{6} \right ) f_d$$
上式中:a和b均为段,即a=a/λ,b=b/λ。
当缓和曲线始点(ZH) 1位于点时,此时a=0、b=1则:
$$
f_1=\frac{1}{6} \times f_d \\
f_2=f_d$$
例:缓和曲线20m弦正矢递变率fd=30mm,1测点和2测点距ZH点分别为a=7.5m,b=2.5m,求f1和f2
弦长为20m,那么点间距λ=10,则a=7.5/10=0.75,b=2.5/10=0.25。
$$f_1=\frac{b^3}{6}f_d=\frac{0.25^3}{6}\times 30=0.1mm\\
f_2=\left (b+\frac{a^3}{6} \right )f_d=\left (0.25+\frac{0.75^3}{6} \right )\times 30=9.6mm$$
2.4 缓和曲线终点(HY、 YH) 相邻两点的正矢
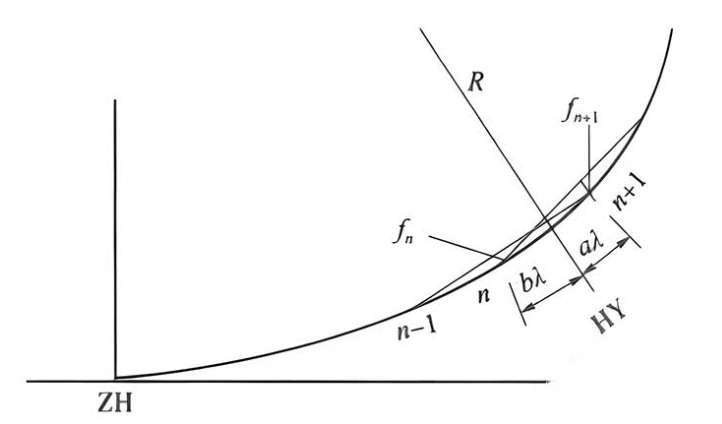
如图所示,n和n+1为与缓圆点相邻的两个测点,距缓圆点分别为bλ和aλ。
则:
则\(f_n=f_y-\frac{1}{6}f_d\)
$$f_{n+1}=f_y$$
当缓和曲线始点(ZH)位于1n点时,a=1、b=0
则
$$f_n=f_y-\left (b+\frac{a^3}{6}\right )f_d$$
$$f_{n+1}=f_y-\frac{b^3}{6}f_d$$
即当缓和曲线始点(ZH)位于测点时,其正矢为圆曲线正矢减缓和曲线正矢递诚变率的六分之一。
例:圆曲线20m弦计划正矢fy=90mm,缓和曲线正矢递减变率fd=30mm,设n测点距HY点距离为7.5m,n+1测点距HY点距离为2.5m,求fn和fn+1。
弦长为20m,那么点间距λ=10,则a=2.5/10=0.25,b=7.5/10=0.75。
解:
$$f_n=f_y-\left ( b+\frac{a^3}{6}f_d\right )=90-\left ( 0.75+\frac{0.25^3}{6}\times 30\right )=67.4mm$$
$$ f_{n+1}=f_y-\frac{b^3}{6}f_d=90-\frac{0.75^3}{6}\times 30=87.9mm$$