圆曲线正矢计算 直圆邻测点正矢计算 直缓邻点正矢计算 缓圆邻点正矢计算 一弦法正矢计算 圆曲线任意矢距计算 曲线正矢计算(有缓) 曲线正矢计算(无缓)

跳过导航链接

缓圆邻点正矢计算

本数据计算依据具体详见缓圆点与圆缓点内、外邻点正矢在线计算注：距离a为示意图中1点至ZH点建的距离；距离b为示意图中2点至ZH点建的距离。

主要参数:
曲线半径R(m): 缓和曲线长(m): 弦长C(m):
距 离 a(m): 距 离 b(m):
fn 正 矢(mm):
fn+1 正 矢(mm):

2.4 缓和曲线终点(HY、 YH) 相邻两点的正矢

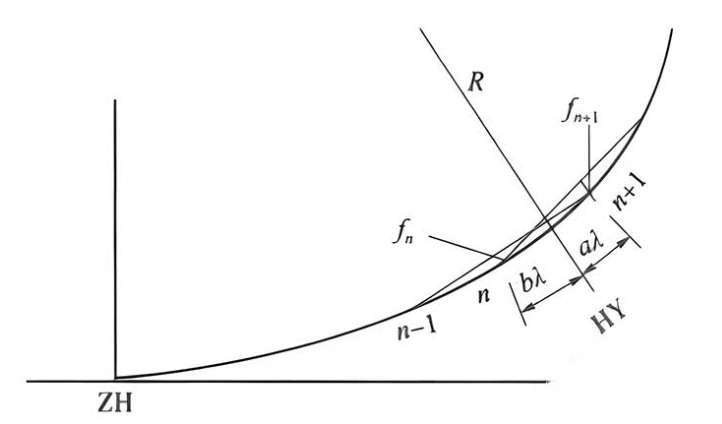
如图所示，n和n+1为与缓圆点相邻的两个测点，距缓圆点分别为bλ和aλ。
则：

则\(f_n=f_y-\frac{1}{6}f_d\)

$$f_{n+1}=f_y$$

当缓和曲线始点(ZH)位于1n点时，a=1、b=0

则
$$f_n=f_y-\left (b+\frac{a^3}{6}\right )f_d$$

$$f_{n+1}=f_y-\frac{b^3}{6}f_d$$

即当缓和曲线始点(ZH)位于测点时，其正矢为圆曲线正矢减缓和曲线正矢递诚变率的六分之一。
例:圆曲线20m弦计划正矢fy=90mm,缓和曲线正矢递减变率fd=30mm,设n测点距HY点距离为7.5m，n+1测点距HY点距离为2.5m，求fn和fn+1。

弦长为20m，那么点间距λ=10，则a=2.5/10=0.25，b=7.5/10=0.75。

解:

$$f_n=f_y-\left ( b+\frac{a^3}{6}f_d\right )=90-\left ( 0.75+\frac{0.25^3}{6}\times 30\right )=67.4mm$$
$$ f_{n+1}=f_y-\frac{b^3}{6}f_d=90-\frac{0.75^3}{6}\times 30=87.9mm$$